Scenery

Landscape

Rocks

Hills

Trees

Water ways

Roads

Structures

Viaducts

This section is about the geometric design of the viaduct at the back of module 2 of my TT model railway. The viaduct resembles the in 1999 abandoned 'Laskitzer Viadukt' of the Tauernbahnwith a length of 93m (TT gauge 775mm).

The length of the viaduct for TT model railway is 562mm. In the real world this would be:

$$\begin{array}{ccc}L& =& L_{\mathit{TT}}\cdot 120\cdot {10}^{-3}\hfill \\ & =& 562\cdot 120\cdot {10}^{-3}\hfill \\ & =& 67.44m\hfill \end{array}$$

At least four arches are required for a realistic look. The width of the arches are between 16 and 20 m on the Tauernbahn. With a span width of 16 m there will not be enough space:

$$67.44-4\cdot 16=3.44m$$

A length of 3.44 meters is not enough for five pillars. After some experimenting 14 meter seems to be the optimal span width of the arches.

The span width of the arch S_TT in TT scale is:

$$\begin{array}{ccc}{S}_{\mathit{TT}}& =& \frac{S}{120\cdot {10}^{-3}}\hfill \\ & =& \frac{14}{120\cdot {10}^{-3}}\hfill \\ & =& 118\mathit{mm}\hfill \end{array}$$

Based on a span width of 14 meters the width of the pillar heads W is:

$$\begin{array}{ccc}W& =& k_w\sqrt{S}\hfill \\ & =& 0.55\sqrt{14}\hfill \\ & =& 2.058m\hfill \end{array}$$

Where:

The width of the pillar heads W_TT for TT scale is:

$$\begin{array}{ccc}{W}_{\mathit{TT}}& =& \frac{W}{120\cdot {10}^{-3}}\hfill \\ & =& \frac{2.058}{120\cdot {10}^{-3}}\hfill \\ & =& 18\mathit{mm}\hfill \end{array}$$

The total length of the viaduct in TT scale L_TT with five pillars and four arches is, as stated before:

$$\begin{array}{ccc}{L}_{\mathit{TT}}& =& 4S_{\mathit{TT}}+5W_{\mathit{TT}}\hfill \\ & =& 4\cdot 118+5\cdot 18\hfill \\ & =& 562\mathit{mm}\hfill \end{array}$$

The increase of the width towards the base of the pillar depends on the slope and the height of the pillar. If the pillar is 9.5 meter high, the offset O is:

$$\begin{array}{ccc}O& =& k_{o}H\hfill \\ & =& 0.03\cdot 9.5\hfill \\ & =& 0.285m\hfill \end{array}$$

Where:

The offset at one side of the 9.5 meter high pillar is in the scale of TT gauge:

$$\begin{array}{ccc}{O}_{\mathit{TT}}& =& \frac{O}{120\cdot {10}^{-3}}\hfill \\ & =& \frac{0.285}{120\cdot {10}^{-3}}\hfill \\ & =& 2.375\mathit{makes}\mathit{rounded}2.5\mathit{mm}\hfill \end{array}$$

The height between the base of the sleepers and the vertex of the arch depends on the width of the arch. This is 14 meters but it is aesthetically more pleasing to use a span width of 16 meter to calculate this height for the 'Mölltheuer' or 'Litzelsdorfer Viadukt' .

$$\begin{array}{ccc}D& =& k_{d}S\hfill \\ & =& 0.09\cdot 16\hfill \\ & =& 1.44m\hfill \end{array}$$

Where:

The dimension between the vertex of the 14 meter arch and base of the sleepers in the scale of TT gauge is:

$$\begin{array}{ccc}{D}_{\mathit{TT}}& =& \frac{D}{120\cdot {10}^{-3}}\hfill \\ & =& \frac{1.44}{120\cdot {10}^{-3}}\hfill \\ & =& 12\mathit{mm}\hfill \end{array}$$

The dimensions for the cross section are measured from photos with viaducts like the one below:

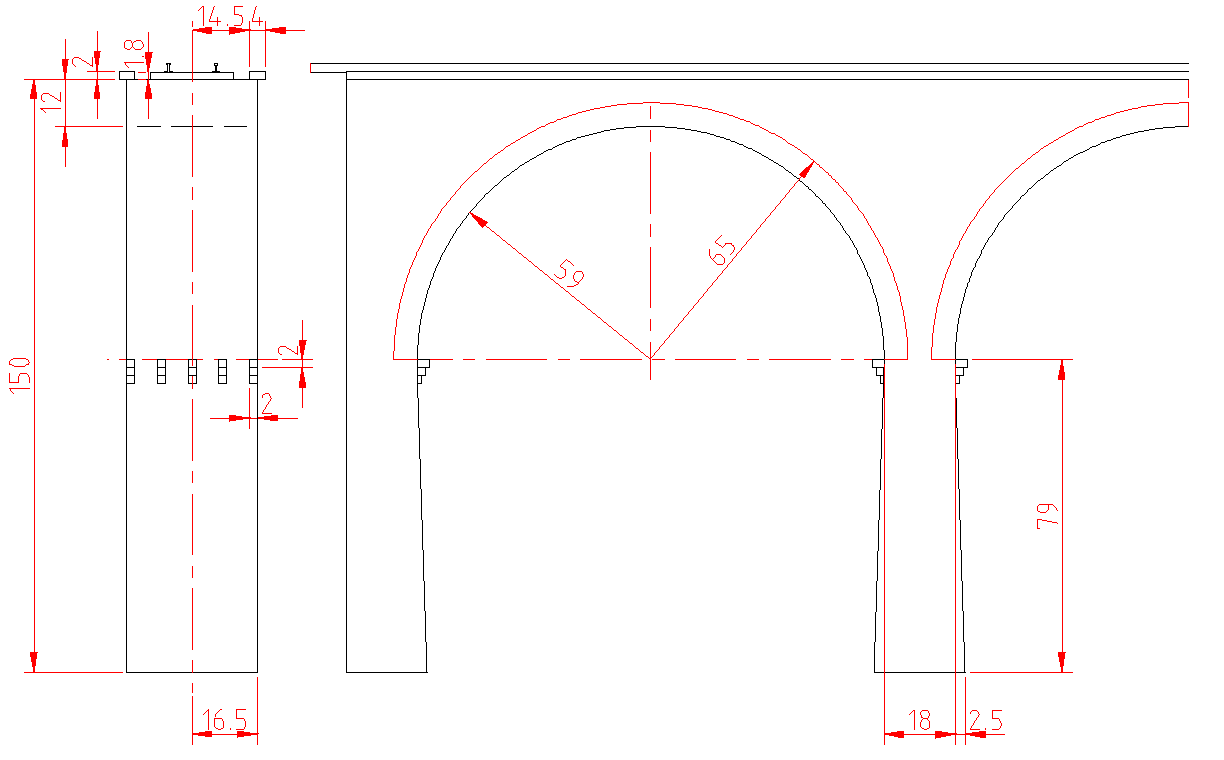
Measurements of the stones in TT scale:

1. Arch:
   1. The stone height:
      H_a(TT) = H_a/120 = 483 / 120 = 4 mm
   2. The width of the arch:
      W_a(TT) = W_a/120 = 995 / 120 = 8 mm
2. Viaduct body and pillars
   1. The average stone height:
      H_ave(TT) = H_ave/120 = 242 / 120 = 2 mm
   2. The maximum stone height:
      H_max(TT) = H_max / 120 = 484 / 120 = 4 mm
   3. The minimum stone height:
      H_min(TT) = H_min / 120 = 80 / 120 = 0.7 mm
   4. The average stone length:
      L_ave(TT) = L_ave / 120 = 500 / 120 = 4 mm
   5. The maximum stone length:
      L_max(TT) = L_max / 120 = 1000 / 120 = 8.5 mm
   6. The minimum stone length:
      L_min(TT) = L_min / 120 = 242 / 120 = 2 mm

Prestressed concrete bridges

This section is about the geometric design of two prestressed concrete bridges at the back and side of module 1 of the TT model railway. The viaduct resembles the 'Moserrinne Brücke' with a length of 150m (TT gauge 1250mm) and the arch of the 'Falkenstein-Brücke' in de direction of Schwarzach with a length of 120m (TT gauge 1000mm) both of the Tauernbahn.

Tunnels